排序算法之堆排序

####简介
学习这个算法之前，首先需要知道什么是堆，以及二叉树的一些特点。
堆：是一颗完全二叉树，并且任一节点的值都要求大于（小于）子节点的值。
完全二叉树具有如下特点：
对于tree[i]，有如下特点：
（1）若i为奇数且i>1，那么tree的左兄弟为tree[i-1]；
（2）若i为偶数且i<n，那么tree的右兄弟为tree[i+1]；
（3）若i>1，tree的父亲节点为tree[i div 2]；
（4）若2\*i<=n，那么tree的左孩子为tree[2\*i]；若2\*i+1<=n，那么tree的右孩子为tree[2\*i+1]；
（5）若i>n/2,那么tree[i]为叶子结点（对应于（3））；
（6）若i<(n-1)/2.那么tree[i]必有两个孩子（对应于（4））。
（7）满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。
完全二叉树第i层至多有2^（i-1）个节点，共i层的完全二叉树最多有2^i-1个节点。
####实现
知道了上面的知识，那么现在就可以来实现堆排序了。
首先，任何一个数组，我们都可以把它看成是一颗完全二叉树，比如：
int[] arr = {2, 5, 3, 10, 6, 9, 7, 8};
可以看成是：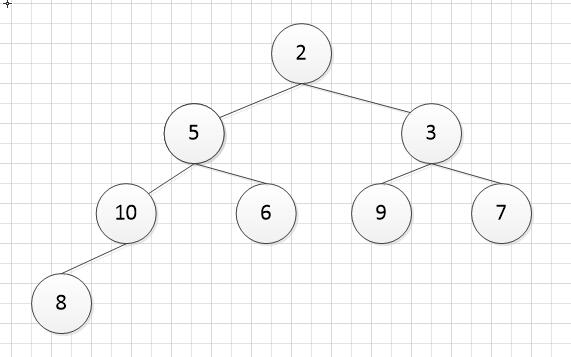
![QQ截图20180321141547.jpg](https://0o0.me/usr/uploads/2018/03/1727065773.jpg)
很显然，它不是一个堆结构，在这里，我实现的是从小到大的排序，所以首先需要将它调整为一颗大顶堆。
调整方法：
* 从最后一个非叶子节点（length / 2 - 1）开始，这里即 arr[3] = 10 的那个节点
* 将节点与其子节点比较，将最大的子节点与其比较，若最大的子节点比它大，则交换，这里显然 8 < 10，所以不用交换
* 再次找到倒数第二个非叶子节点 arr[2] = 3，存在最大子节点 9 > 3，将其交换，此时树结构如下：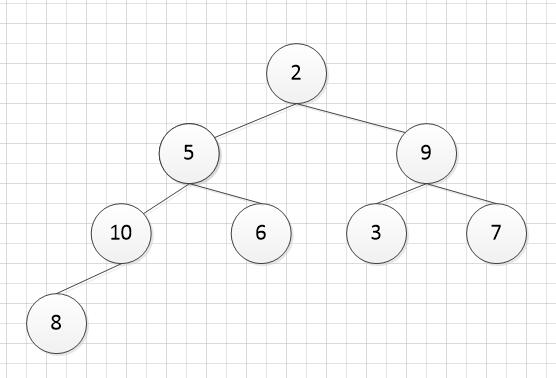
![QQ截图20180321142248.jpg](https://0o0.me/usr/uploads/2018/03/384835047.jpg)
* 继续非叶子节点 arr[1] = 5，将其与最大子节点 10 交换，交换后如下：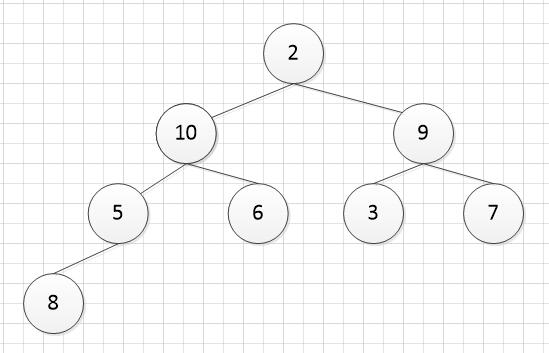
![QQ截图20180321142453.jpg](https://0o0.me/usr/uploads/2018/03/3132386489.jpg)
* 此时注意，先别急着去找 arr[0] = 2 这个非叶子节点，因为此时交换后非叶子节点 arr[3] = 5 出现了存在比它大的节点 arr[7] = 8，所以必须先将其先交换调整，这一点在下面的代码中`i = max`可以体现的出来。
* 按照上面的思路最终调整的大顶堆如下：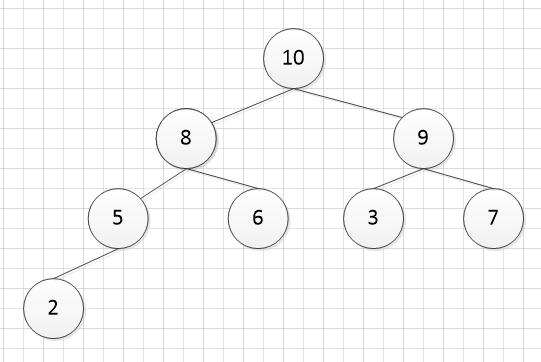
![QQ截图20180321143101.jpg](https://0o0.me/usr/uploads/2018/03/4148072708.jpg)

此时，数组顺序为：10 8 9 5 6 3 7 2
可以看到，还是无序的，接下来要做的就是真正的排序了，思路如下：
* 将大顶堆的根元素（即当前堆的最大元素）与数组末尾元素交换，即把最大值放置数组末尾
* 交换过后，最后一个数不用排序了，继续把前面 length - 1 个数当成一个数组，重新调整为大顶堆
* 重复第一个步骤，但此时的数组末尾是相对于数组的 length - 1 - i 的位置

注释里也有详细解释，实现代码：
```java
public class HeapSort {

private int[] arr;

private void sort() {
		//从最后一个非叶子节点（length/2-1）开始调整为大顶堆
		for (int i = arr.length / 2 - 1; i >= 0; i--) {
			adjustHeap(i, arr.length);
		}
		System.out.println("初始化大顶堆：");
		print();
		//把大顶堆最大值放到数组最后
		for (int i = 0; i < arr.length; i++) {
			//每次将堆顶最大值放到数组末尾（这个末尾是相对的，并不是指数组的最后一个元素，而是数组未排序部分的最后一个元素）
			swap(0, arr.length - 1 - i);
			System.out.println("第"+i+"次交换");
			print();
			//交换过后需将未排序部分的数组重新调整为大顶堆
			adjustHeap(0, arr.length - 1 - i);
			System.out.println("交换后重新调整的大顶堆：");
			print();
		}
	}

private void adjustHeap(int i, int length) {
		int left = i * 2 + 1;   //左叶子节点数组下标
		while (left < length) { //必须存在左叶子节点，即自身必须为非叶子节点
			int right = left + 1;
			int max = left;     //左右叶子较大者的位置
			//是否存在右叶子节点，并且右叶子大于左叶子节点,则改变max的值
			if (right < length && arr[right] > arr[left]) {
				max = right;
			}
			//若叶子节点较大者比父节点大，则交换
			if (arr[max] > arr[i])  {
				swap(max, i);
			}
			//交换过后可能需要再次调整，因为调整过后不能确保当前叶子节点的值比它的叶子节点都大，如下面注释情况
			i = max;
			left = i * 2 + 1;
		}
	}

/**
	 * arr[0] = 20, arr[1] = 30, arr[2] = 10, arr[3] = 25, arr[4] = 15
	 *
	 *             20                               30                         30
	 *            *  *                             *  *                       *  *
	 *           *    *      30与20交换            *    *     20与25交换      *     *
	 *          30    10     --------->          20     10   --------->     25     10
	 *         *  *          i=0, max=1         *  *                       *  *
	 *        *    *                           *    *                     *    *
	 *       25    15                         25    15                   20    15
	 *          （一）                             （二）                      （三）
	 *
	 * 若以上（一）到（二）交换过后退出了循环，那么大顶堆将调整失败，因为存在叶子节点 25 大于 20 父节点，所以此时必须把 i 赋值为 1，
	 * 即非叶子节点 arr[1] = 20 需再次做调整，最后调整结果如（三）所示。
	 */

public static void main(String[] args) {
		HeapSort hs = new HeapSort();
		hs.init();
		System.out.println("初始数组顺序.");
		hs.print();
		hs.sort();
		System.out.println("排序后数组顺序.");
		hs.print();
	}

private void init() {
		/*Random random = new Random();
		arr = new int[10];
		for (int i = 0; i < arr.length; i++)
			arr[i] = random.nextInt(100);*/
		arr = new int[]{2, 5, 3, 10, 6, 9, 7, 8};
	}

private void print() {
		for (int a : arr)
			System.out.print(a + " ");
		System.out.println();
	}

private void swap(int a, int b) {
		int temp = arr[a];
		arr[a] = arr[b];
		arr[b] = temp;
	}
}
```

排序算法之堆排序

发表评论：